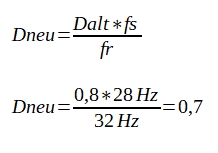Berechnung eines Transmissionline-Gehäuses (TML) mit meiner Tabellenkalkulation

Eine Transmissionline mit einem einfachen ungedämpften Rohr würde ein sehr großes Gehäuse mit einem welligen Frequenzgang zur Folge haben. Ein gut abgestimmter Transmissionline Lautsprecher aber, hat einen tief reichenden Bass und eine sonst unerreichte Impulswiedergabe im Tiefbassbereich. Auch Chassis mit einem Qts>0,5 , die für eine Bassreflex-Box ungeeignet sind, können in einer Transmissionline Box verwendet werden. Ein geschlossenes Gehäuse geht zwar auch, hat aber nicht den tiefen Bass!
Von Arthur R. Bailey und Martin J. King wurden physikalische Effekte entdeckt, die man nutzen kann um die Länge der TML und die Oberwellen einer Transmissionline zu reduzieren, damit sich ein linearer Frequenzgang ergibt. Die Kalkulation des Versatzes und die Verteilung des Dämpfungsmaterials konnte ich weiter entwickeln und verbessern! Ich habe diese Prinzipien mit dem Versatz (Offset) des Bass-Chassis genutzt um mit komplexen Formeln die Gehäuseabmessung und die Verteilung des Dämpfungsmaterials im Transmissionlinekanal zu berechnen. Die Simulation des Frequenzganges war nicht mein Thema!
Die komplette mathematische Ableitung der Formeln möchte ich hier nicht darstellen, was im Netz fehlt... ist eine einfache aber genaue Berechnung des Transmissionline-Gehäuses. Um meine Formeln zu überprüfen hatte ich eine Tabellenkalkulation erstellt, da die manuelle Überprüfung der komplexen Formeln sehr aufwendig und fehlerbehaftet ist. Diese Tabellenkalkulation habe ich erweitert und ergänzt damit sie von den normalen Anwendern einfach angewendet werden können.
Viele Formeln, die man so im Netz findet, gehen nach dem Prinzip "Pi mal Daumen" und damit ist ein Scheitern der Konstruktion vorprogrammiert! Genau so sind viele Voraussetzungen und Angaben, die man für ein TML-Gehäuse findet längst überholt. Ich habe da auch meine Erfahrungen machen müssen und deswegen die Formel/Tabellenkalkulation zu dem Thema entwickelt.
Wie so oft sitzt das Problem dann bei der praktischen Umsetzung. Weil die Dämpfung bei der Line sehr wichtig ist, habe ich auch einen Dämpfungsplan erstellt, der genau die Abschnitte in der Line angibt, die stärker bedämpft werden müssen. Daher ist auch die Simulation einer TML sehr schwierig, weil eine starke Abhängigkeit zur Dämpfung besteht.
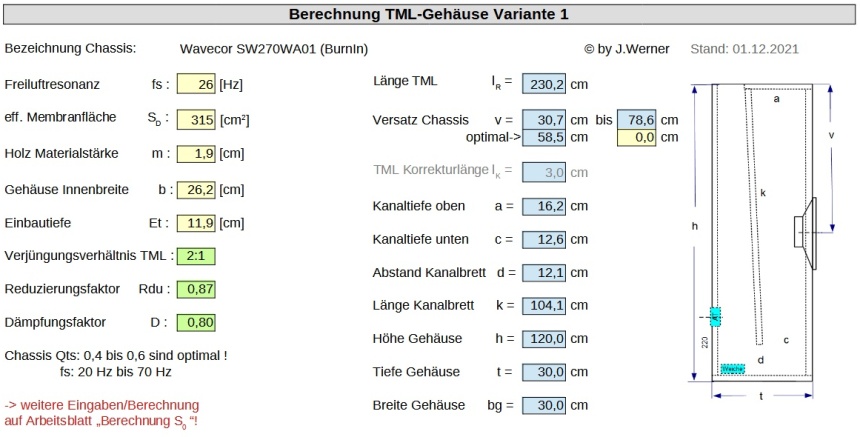
Für die Berechnung der Transmissionline muss man nur die Daten der gelben Felder der Tabellenkalkulation, wie unten im Bild zu sehen ist, bearbeiten!
|
|
Unter dem Punkt Verjüngungsverhältnis TML kann man den Verjüngungsfaktor "1,5:1", "2:1", "3:1", "5:1" oder "10:1" auswählen. Höhere Verjüngungsfaktoren TML (S0/SL) "10:1" oder "5:1" sind gerade bei Subwoofern und bei sehr tiefer Abstimmung nahe 20 Hz sinnvoll, da das Gehäuse sehr hoch wird. Durch Optimierung der Berechnung wird das Gehäuse nur geringfügig etwas tiefer 😉 Anleitung Gehäusebau ! Die Line wird normalerweise auf die Freiluftresonanzfrequenz fs des Chassis abgestimmt, bei einem nicht so optimalem Qts ist eine abweichende Abstimmung mit fr sinnvoll. Die Berechnung der optimalen Resonanzfrequenz fr auf dem Arbeitsblatt "Berechnung S0" ist neu hinzu gekommen und muss manuell durch die Eingabe bestätigt werden. Anstatt mit fs werden dann die Gehäusemaße mit fr berechnet. Die von mir verwendeten Vorgaben liefern ein praxisnahes Ergebnis mit praktischen Gehäusegrößen. Meine Kalkulation nutzt erstmals zu dem Thema die drei Effekte nach Bailey und King, um einen linearen Tiefbass zu erzeugen. Gehäusevarianten sind im Rahmen der Abmessungen möglich, wie das Beispiel oben TwinBambu zeigt.
Weitere berechnete Beispiele:
TML-Gehäuse für Morel CAW 938 : Dieses Chassis ist nur für eine TML geeignet, erreicht aber mit seinen 22,2cm Durchmesser eine sagenhafte Grenzfrequenz f3=21Hz! Maße: 125x30x42 cm (HxBxT), Verj.TML="1,5:1", 8 Ω !
TML-Gehäuse für Visaton TIW200XS : Dieses Subwoofer-Chassis mit 22,2cm ∅ erreicht f3=25Hz mit erträglichen Abmessungen 113x28x32 cm, (HxBxT), Verj.TML="1,5:1", 8 Ω, Sandwichmembran aus mehreren Glasfaserschichten!
TML-Gehäuse für Wavecor SW215WA01 : Ein Subwoofer-Chassis mit 21,5cm ∅ erreicht knapp f3=24Hz mit einem Aufschlag von 24% ein schmales Gehäuse mit den Maßen: 115x25x25 cm (HxBxT), Verj.TML="1,5:1", 4 Ω ! Schafwolle ist bei Amazon erhältlich!
TML-Gehäuse für Peerless SLS 10-39/08 P830668 : Dieses Chassis mit 26,2cm ∅ erreicht f3=22Hz mit den Maßen: 117x35x36 cm (HxBxT), Verj.TML="1,5:1", 8 Ω !
TML-Gehäuse für ScanSpeak 26W-8534G00 : Dieses Chassis mit 27,2cm ∅ erreicht f3=22Hz mit den Maßen: 140x32x45 cm (HxBxT), Verj.TML="1,5:1", 8 Ω !
TML-Gehäuse für ScanSpeak 25W8565-00 : Dieses Chassis mit 25,5cm ∅ wurde wohl für ein TML-Gehäuse entwickelt. Es erreicht f3=20Hz mit den Maßen: 148x35x47 cm (HxBxT), Verj.TML="2:1", 8 Ω !
TML-Gehäuse für MONACOR SP-252E : Jetzt noch ein sehr günstiges Chassis mit 25,5cm ∅. Trotz einem Qts=0,5 und 4 Ω erreicht es nur ein f3=30Hz mit den Maßen: 89x30x59 cm (HxBxT), Verj.TML="1,5:1"!
Das hier im Beispiel verwendete Chassis Wavecor SW270WA01 4 Ω, erreicht mit fr=24,6Hz eine sehr gute untere Grenzfrequenz f3=19,6Hz mit den Maßen: 135x30x31 cm (HxBxT), Verj.TML="1,5:1" !.
Die Beispiele zeigen deutlich, dass es nicht nur auf eine kleine Membranfläche ankommt. Sondern die Impedanz sollte bei 4 Ω und der Qts-Wert mit >0,4 etwas höher liegen. Die Gehäuse in den Beispielen haben die gleiche Breite (30cm) aber die Gehäusetiefe ändert sich auf Grund der Parameter der Chassis:
Eton 8-402-C8-32 Hex : 222 cm2; 27 Hz; 8 Ω; Qts=0,47 -> Tiefe=36,6 cm
Dayton RS270-8 : 346 cm2; 30 Hz; 8 Ω; Qts=0,47 -> Tiefe=59,5 cm
SEAS CA22RNX H1288 : 230 cm2; 29 Hz; 8 Ω; Qts=0,41 -> Tiefe=56,8 cm
ScanSpeak 22W-8534G00: 235 cm2; 30 Hz; 8 Ω; Qts=0,40 -> Tiefe=47,1 cm
ScanSpeak 26W-8534G00: 350 cm2; 23 Hz; 8 Ω; Qts=0,40 -> Tiefe=47,1 cm
TangBand W8-750C : 220 cm2; 30 Hz; 8 Ω; Qts=0,43 -> Tiefe=36,6 cm
Wavecor SW270WA01 : 315 cm2; 28 Hz; 4 Ω; Qts=0,50 -> Tiefe nur 30 cm ... mit Aufschlag !
Eigentlich würde man ja davon ausgehen, dass die kleinste Membranfläche auch die kleinste Box erzeugt ... das ist aber nicht so!
Die Gehäusehöhe wird hauptsächlich durch die Resonanzfrequenz fs, Dämpfungsfaktor D und Reduzierungsfaktor Rdu bestimmt! Sie ist im Wohnzimmer meistens unkritisch, nur die Grundfläche mit Breite und Tiefe sollte möglichst klein sein.
Parameter für eine kleine Grundfläche der Box:
-> Impedanz: 4 Ω
-> eine kleine Membranfläche (ansonsten gilt ... je größer desto besser)
-> Qts: 0,5 bis 0,7
-> Kraftfaktor BxL möglichst groß aber nicht zu groß (BxL<13 bei 4 Ω)
-> niedrige Freiluftresonanz fs nahe bei 20 Hz
Natürlich muss man bei der Auswahl des Bass-Chassis für die Line Kompromisse eingehen, da alle Parameter gleichzeitig optimieren geht nicht! Dabei ist eine kleine Grundfläche nicht das einzige Ziel, wichtige andere Parameter wie z.B. Pegelfestigkeit und niedrige Verzerrungen spielen auch eine Rolle. Es gibt hochwertige 8 Ohm Bass-Chassis mit einer günstigen Parameter-Kombination, die gute Ergebnisse liefern.
Neu hinzu gekommen ist auf dem Arbeitsblatt "Berechnung S0" die Ermittlung der unteren Grenzfrequenz f3 (-3dB) , die optimale Resonanzfrequenz fr und die Pegeldifferenz zum Kennschalldruck in Abhängigkeit von Qtd, Dämpfungsfaktor D und Verjüngungsverhältnis TML. Dieser Wert ist natürlich auch noch von dem eigentlichen Frequenzgang des Bass-Chassis abhängig und soll einen Anhaltspunkt bieten, wird aber für den Normalfall passen. Zusätzlich wird die Pegelabweichung zum Kennschalldruck im Tiefbassbereich bis ca. 100 Hz angegeben.
|
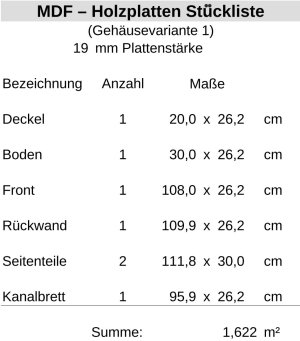
Auf der nächsten Seite wird die Stückliste 1 der Gehäusebauteile zusammengestellt !
 Durch die unterschiedliche Qualität der Materialien, Produktionsabweichung der Chassis und ungenaue Ausführung der Arbeiten kann es zu Abweichung der berechneten Resonanzfrequenz der Transmissionline kommen! In gewissen Grenzen kann man eine Korrektur der Dämpfung über den Dämpfungsfaktor durchführen und das Dämpfungsmaterial erhöhen bzw. verringern! Durch die unterschiedliche Qualität der Materialien, Produktionsabweichung der Chassis und ungenaue Ausführung der Arbeiten kann es zu Abweichung der berechneten Resonanzfrequenz der Transmissionline kommen! In gewissen Grenzen kann man eine Korrektur der Dämpfung über den Dämpfungsfaktor durchführen und das Dämpfungsmaterial erhöhen bzw. verringern!
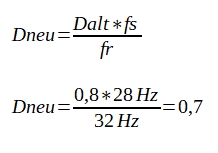
Hier im Beispiel: Die gemessene Resonanzfrequenz fr=32 Hz ist zu hoch!
Dneu eingeben -> neue Menge = 397 g (vorher 307 g)
Die Gehäuseabmessungen des Lautsprechers bleiben natürlich dann gleich, nur die Dämpfung wird über die Menge des Dämpfungsmaterials in den jeweiligen Abschnitten geändert! Aber vorher die Messung überprüfen, war z.B. ein Subsonic-Filter aktiv und Wohnraummessungen mit Sinus-Signalen verfälschen die Messwerte.
Nach dem Prinzip Bailey -> Änderung der Dämpfung -> Änderung der Schallgeschwindigkeit in der Line! Sollte der Tiefbass zu schwach sein, kann man die Intensität der Dämpfung über den Dämpfungsfaktor bearbeiten. Wenn der Tiefbass zu stark ist, reicht es aus, wenn man im letzten Abschnitt das Dämpfungsmaterial immer wieder verdoppelt und zwischendurch mal prüft, ob das Ergebnis den eigenen Wünschen entspricht. Also hier im Beispiel:
von 5 g -> 10 g "testen" -> 20 g "testen" -> 40 g "testen" -> 80 g ! max. 4x verdoppeln!
Tipps für den Aufbau:
Das Mittel-Hochton-Gehäuse sollte auf die Front oder obendrauf gebaut werden, damit es möglichst wenig Störungen im TML-Kanal gibt. Falls doch, dann das Gehäuse oder die Weiche möglichst schmal bauen und von oben nach unten verlegen. Auch Aufschläge auf die Kanalfläche vermindern die Störung, je größer das Verhältnis Am/SD ist, desto geringer wirken sich Störungen aus!
Unterstützen Sie mich!
|
|
Der Dämpfungsfaktor bestimmt die Dichte der Schafwolle im TML-Kanal und hat damit Einfluss auf die untere Grenzfrequenz f3, den Schalldruck-Pegel, die Linearität im Tiefbassbereich und die Gehäusehöhe. Der Standardwert D=0,8 stellt dabei einen guten Kompromiss dar, in nachfolgender Tabelle werden die Auswirkungen bei abweichender Einstellung dargestellt.
| Dämpfungsfaktor D |
Einstellbereich
0,6 - 0,8 - 1 |
untere Grenz-
frequenz f3 |
Schalldruck-
pegel |
Linearität im
Tiefbass |
Gehäuse-
Höhe |
Gehäuse-
Tiefe |
| D > 0,8 |
↓ tiefer |
↑ höher |
↓ geringer |
↑ höher |
→ gleich |
| D < 0,8 |
↑ höher |
↓ tiefer |
↑ höher |
↓ geringer |
→ gleich |
| |
|
|
|
|
|
| Der Wert D=1 bedeutet dabei keine Dämpfung (ohne Schafwolle). Über den Dämpfungsfaktor lässt sich nachträglich die Intensität im Tiefbass regeln. Auch können Bass-Chassis mit Qts-Werten bei 0,7 mit D=0,6 so stark gedämpft werden, dass es zu keiner Bassüberhöhung kommt. |
| |
|
|
|
|
|
| Verjüngungsverhältnis TML |
|
Verj. TML <2:1
|
∼ gleich |
↑ höher |
↓ geringer |
↑ höher |
etwas ↓ |
| Verj. TML >2:1 |
etwas ↑ |
↓ geringer |
↑ höher |
↓ geringer |
etwas ↑ |
Die höheren Verjüngungsverhältnisse 3:1; 5:1 und 10:1 bieten sich bei Subwoofern und bei einer sehr tiefen Abstimmung fr bei 20Hz an, da das Gehäuse sehr hoch wird! Hier ein Beispiel mit dem ScanSpeak 25W856500 abgestimmt auf 20Hz. ( Maße in cm ) |
| |
|
|
Verjüngungsv. |
Höhe |
Tiefe |
| |
|
|
1,5:1 |
165,8 |
45,5 |
| Man sieht sehr deutlich, dass sich die Tiefe |
2:1 |
155,3 |
45,9 |
| mit steigendem Verjüngungsverhältnis nur |
3:1 |
143,7 |
45,8 |
| nur geringfügig steigert! |
5:1 |
128,8 |
46,6 |
| |
|
|
10:1 |
114,2 |
49,1 |
|
|
Man kann mit den Werten Resonanzfrequenz fr, Verjüngungsfaktor TML und Dämpfungsfaktor D vorsichtig jonglieren um dadurch eine optimale Abstimmung für die TML zu finden.
Hier noch ein Beispiel:
Die Einstellungen D=0,8; Verj.TML=2:1; fr=fs=26Hz und Aufschlag=8% liefern eine Pegeldifferenz von +0,54dB und f3=21Hz.
1. Möglichkeit: fr=25,3Hz einstellen ergibt eine Pegeldifferenz +0,06dB und f3=21Hz.
2. Möglichkeit: D=0,77 einstellen ergibt eine Pegeldifferenz +0,08dB und f3=21,8Hz.
3. Möglichkeit: Verj.TML=3:1 einstellen ergibt eine Pegeldifferenz +0,11dB und f3=21,8Hz.
4. Möglichkeit: Anstatt fr=25,3Hz -> fr=24,6Hz einstellen ergibt eine Pegeldifferenz -0,41dB und f3=20,4Hz.
Dabei ist eine Kombination aller 3 Parameter möglich und die Empfehlung für fr wird automatisch berechnet! Kann aber auch bei Bedarf manuell geändert werden.
Wenn Sie Verj.TML=3:1; fr=24,9Hz und D=0,84 gleichzeitig einstellen, ergibt das eine Pegeldifferenz von 0,0dB und f3=20,4Hz.
Ziel sollte es sein die Pegeldifferenz auf ca. 0dB zu minimieren, um einen linearen Tiefbassbereich zu bekommen.
Da meine Webseite kein Forum hat, würde ich mich über Beiträge unten im Kommentar freuen! Ich hoffe ich konnte einen Beitrag dazu leisten, dass der Bau deiner TML-Box einfacher und ein Erfolg wird.
Alle Angaben und Berechnungen ohne Gewähr! © by J.Werner
|
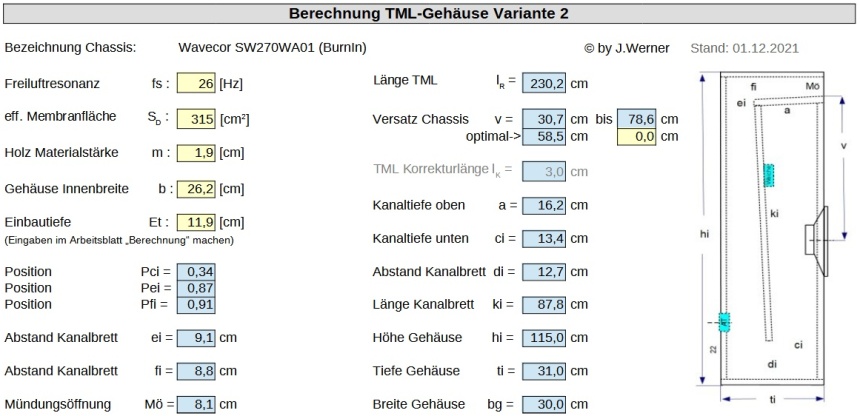





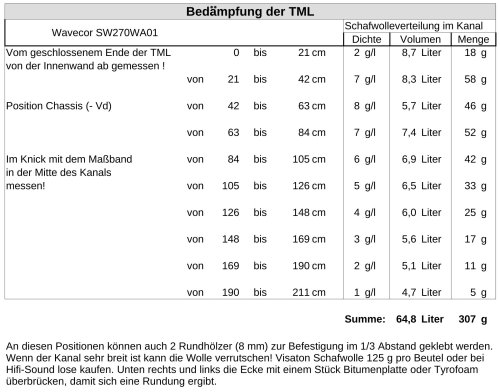 hinter dem Chassis wird das Volumen, welches das Chassis selber benötigt, berechnet und abgezogen! Bitte halten Sie sich an die berechnete Menge Schafwolle. Zur Fixierung der Schafwolle hat sich eine Rolle mit Klettverschlussband bewährt. Einfach ein Stück um die Rundhölzer und in die Seitenflächen kleben und die Schafwolle einhaken (Bild unten).
hinter dem Chassis wird das Volumen, welches das Chassis selber benötigt, berechnet und abgezogen! Bitte halten Sie sich an die berechnete Menge Schafwolle. Zur Fixierung der Schafwolle hat sich eine Rolle mit Klettverschlussband bewährt. Einfach ein Stück um die Rundhölzer und in die Seitenflächen kleben und die Schafwolle einhaken (Bild unten). 

 Durch die unterschiedliche Qualität der Materialien, Produktionsabweichung der Chassis und ungenaue Ausführung der Arbeiten kann es zu Abweichung der berechneten Resonanzfrequenz der Transmissionline kommen! In gewissen Grenzen kann man eine Korrektur der Dämpfung über den Dämpfungsfaktor durchführen und das Dämpfungsmaterial erhöhen bzw. verringern!
Durch die unterschiedliche Qualität der Materialien, Produktionsabweichung der Chassis und ungenaue Ausführung der Arbeiten kann es zu Abweichung der berechneten Resonanzfrequenz der Transmissionline kommen! In gewissen Grenzen kann man eine Korrektur der Dämpfung über den Dämpfungsfaktor durchführen und das Dämpfungsmaterial erhöhen bzw. verringern!